EXPRESIONES RECURSIVAS

“Iterar es humano, recursivizar es divino” (L. Peter Deutsch)

“El quanta de la conciencia es la recursion” (Dan Winter)

“Yo pienso sobre el pensamiento” (Douglas Hofstadter)

---

Definición

Una expresión recursiva es una expresión que hace referencia a sí misma.


Observaciones

• Las expresiones recursivas pueden estar o no parametrizadas.
  
  
• Las expresiones recursivas pueden ser de todo tipo: genéricas, específicas, funciones, secuencias, conjuntos, etc.
  
  
• Las expresiones recursivas simplifican notablemente la especificación, habiéndose utilizado ampliamente en la definición de derivadas como, por ejemplo, en rango, repetición, longitud, profundidad, punto decimal, etc.
  
  
• Las expresiones recursivas pueden evaluarse como una expresión finita o infinita. En este último caso, hay que usar la sustitución potencial (la representación).

Ejemplos

1. Secuencia recursiva:
   
   (x =: (a b c x↓)) // rep. (a b c a b c a b c ...)
x\4 // ev. a
x\5 // ev. b
x\6 // ev. c
x\7 // ev. a
   
   
2. Factorial de n:
   
   ⟨( fac(n) = (1 ← n=0 →' n*fac(n−1) )⟩
fac(4) // ev. 24
   
   
3. Suma de los n primeros componentes de una secuencia x:
   
   ⟨( suma(x n) = (0 ← n=0 →' (suma(x n−1) + x\n) )⟩
(x° = ( 1…100 ))
suma(x 100) // ev. 5050
suma(x 50) // ev. 2525
   
   
4. Torres de Hanoi.
   
   

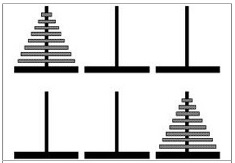
   Torres de Hanoi Posiciones inicial y final

   
   Se tienen n discos (de tamaños 1 a n) insertados, de mayor a menor en un eje A. Se trata de mover los n discos desde el eje A hasta el eje C, usando el eje intermedio B como trabajo, de tal forma que un disco no puede colocarse sobre otro de menor tamaño.
   
   La estrategia de solución es la siguiente:
   
   
   • Se mueven los n−1 discos superiores desde A hasta B, usando el eje de trabajo C.
   • Se mueve el disco n desde A a C.
   • Se mueven los n−1 discos superiores desde B hasta C, usando el eje de trabajo A.
   
   Representaremos el movimiento de un disco i desde el eje x al eje y como (i x y).
   
   Mover n discos desde el eje x al eje z usando el eje de trabajo y

⟨( hanoi(n x y z) = ((1 x z) ← n=1 →’ ( hanoi(n−1 x z y) (n x z) hanoi(n−1 y x z) ) )⟩

hanoi(1 A B C) // ev. ( (1 A C) )
hanoi(2 A B C) // ev. ( (1 A B) (2 A C) (1 B C) )
hanoi(3 A B C) // ev. ( (1 A C) (2 A B) (1 C B) (3 A C) (1 B A) (2 B C) (1 A C) )
   
   
5. Secuencia de Fibonacci:
   
   ⟨( fibo(x y) =: (x y f(x y)) )⟩/⟨( f(u v) = (u+v (f(v u+v))↓ )⟩

fibo(1 1) // rep. (1 1 2 3 5 8 13 ...)
fibo(−5 8) // rep. (−5 8 3 11 14 25 ...)
fibo(a b) // rep. (a b a+b a+2*b a+3*b a+4*b ...)

Números recursivos

Los números más importantes de la matemática tienen estructura recursiva, y por lo tanto indican máxima compresión. Ejemplos:

1. El número π:
   
   

   Fórmula de John Wallis

   
   ( π =: 2*f(2)/⟨( f(n) = (n*n).÷((n−1)*(n+1))*f(n+2) )⟩ )
   
   

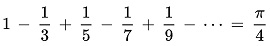
   Fórmula de Gregory-Leibniz

   
   ( π =: 4*f(1 +1)/⟨( f(n s) = (1÷n + 1÷f(n+2 −s)) )⟩ )
   
   

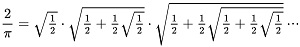
   Fórmula de Viète

   
   ( π =: 2.÷f(k)/⟨( f(n) = (0 ← n=0 →' f(n−1)*(1÷2 + f(n−1))Ú2 ) )⟩ )
   
   
2. El número e:
   
   

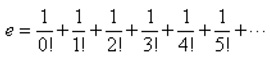
   Fórmula de Euler

   
   ( e =: s(1)/⟨( s(n) = 1÷(1*…*n) + s(n+1) )⟩ )
   
   

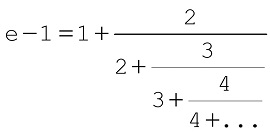
   Fórmula de Ramanujan

   
   ( e =: (1+f(1))/⟨( f(n) = n + (n+1).÷f(n+1)) )⟩ )
   
   
3. Logaritmo neperiano de 2:
   
   
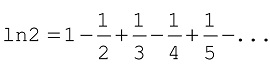
   ( ln(2) = f(1)/⟨( f(n) = 1.÷(n+1) + f(n+2) )⟩ )

Recursión mutua

Se produce cuando dos expresiones se hacen referencia mutuamente. Por ejemplo:

(x =: (a y↓))
(y =: (b x↓)
x // rep. (a b a b ...)
y // rep. (b a b a ...)